Case de Projeto

A empresa Gas Service buscou a OTMZA com o intuito de reduzir a massa da estrutura metálica para uma de suas fornalhas a casca de arroz. A partir da análise das tensões da estrutura, adotou-se uma metodologia para a realização da otimização estrutural com relação à massa, que resultaram em uma geometria que atende aos requisitos e esforços, definidos pelo cliente.

 

Foi utilizada uma análise computacional pelo Método de Elementos Finitos, a partir da teoria estrutural de elasticidade linear, e uma otimização paramétrica, baseada na teoria de otimização por gradiente para a realização das simulações do presente projeto. Para tal, empregou-se o software HyperWorks, licenciado da Altair, para a realização de todas as simulações do projeto. A metodologia em questão foi adotada com o intuito de aumentar a competitividade do produto e facilitar o transporte da estrutura.

Visto que o problema possui componentes com uma dimensão muito maior que as outras duas, a abordagem para a análise e otimização foi utilizar elementos finitos unidimensionais. Assim, nestes elementos, os parâmetros que são inseridos detalham somente os nós inicial e final de cada elemento e a geometria da seção transversal.

Definição da Geometria

Como a disposição dos perfis se manteve, a geometria para otimização estrutural foi definida apenas pela posição dos nós iniciais e finais de cada elemento. O sistema de coordenadas para os perfis de tipo L, W e U estão representados na figura abaixo. Para o posicionamento representativo dos perfis no software foi adotado que a linha que conecta o nó inicial e final de cada elemento passa pela origem (y, z = 0) da representação local de cada seção transversal. Entretanto, o software possui como convenção posicionar os elementos no centro de cisalhamento de cada perfil, que foi ajustado com o comando “offset” para a convenção abordada.

Convenções para posicionamento de perfis

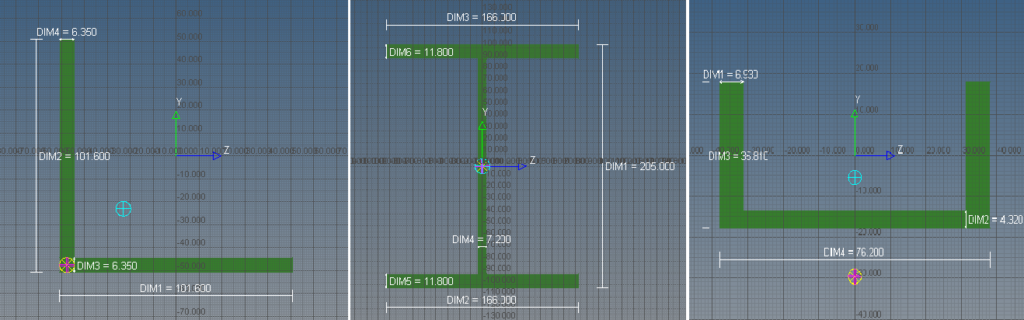
Fonte: OTMZA (2019)

Tendo em vista que tanto a geometria quanto as condições de contorno são simétricas, modelou-se apenas metade da estrutura aplicando condições que representam as conexões nos nós que dividem a simetria. No modelo, representado na figura abaixo, foram aplicadas restrições de movimento translacional no eixo z e rotacional nos outros dois eixos nos nós que conectam a outra metade da estrutura. Como convenção, o software utiliza 1, 2 e 3 para referenciar as translações nos eixos x, y e z, respectivamente, e os valores 4, 5 e 6 para as rotações nos mesmos eixos ordenados da mesma maneira. As restrições são representadas por um triângulo azul, nesse caso, e com os graus de liberdade restringidos simbolizados próximo à cada restrição.

Modelo em elementos finitos representando a geometria com restrições

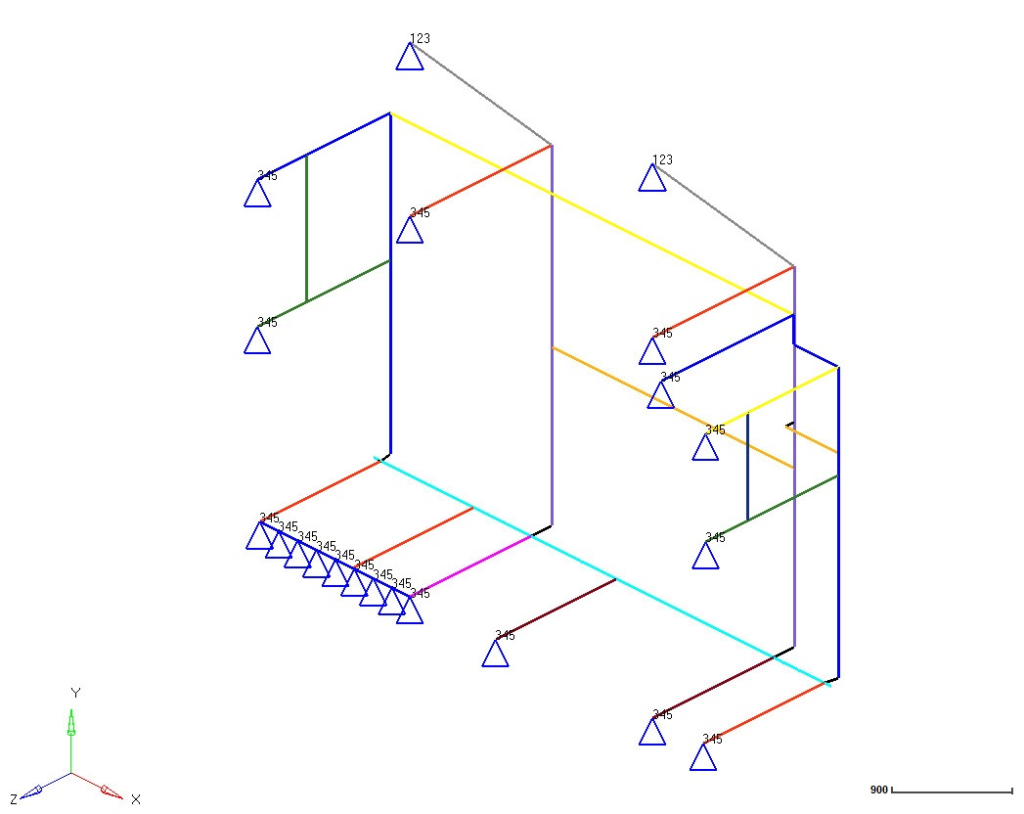
Fonte: OTMZA (2019)

A orientação com relação ao sistema de coordenadas global de cada perfil foi definida resultando no modelo representativo exposto na abaixo. Dessa maneira, todos os elementos foram definidos com propriedade de viga curta de Timoshenko, que consideram todos os esforços possíveis para elementos unidimensionais.

 Modelo em elementos finitos representando a orientação dos perfis

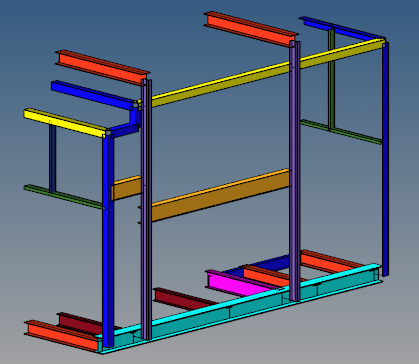
Fonte: OTMZA (2019)

Condições de Contorno

Com o intuito de garantir que a estrutura resista às solicitações impostas durante o processo de transporte da fornalha, foram fornecidas cargas equivalentes para o caso crítico de içamento por cabos.

As cargas impostas aos perfis são distribuídas ao longo de toda a geometria, no modelo computacional isto é convertido para cargas equivalentes aplicadas a cada nó da malha analisada. Esta aproximação possui validade para grande número de nós, como é o caso do modelo simulado.

Modelo em elementos finitos representando os carregamentos

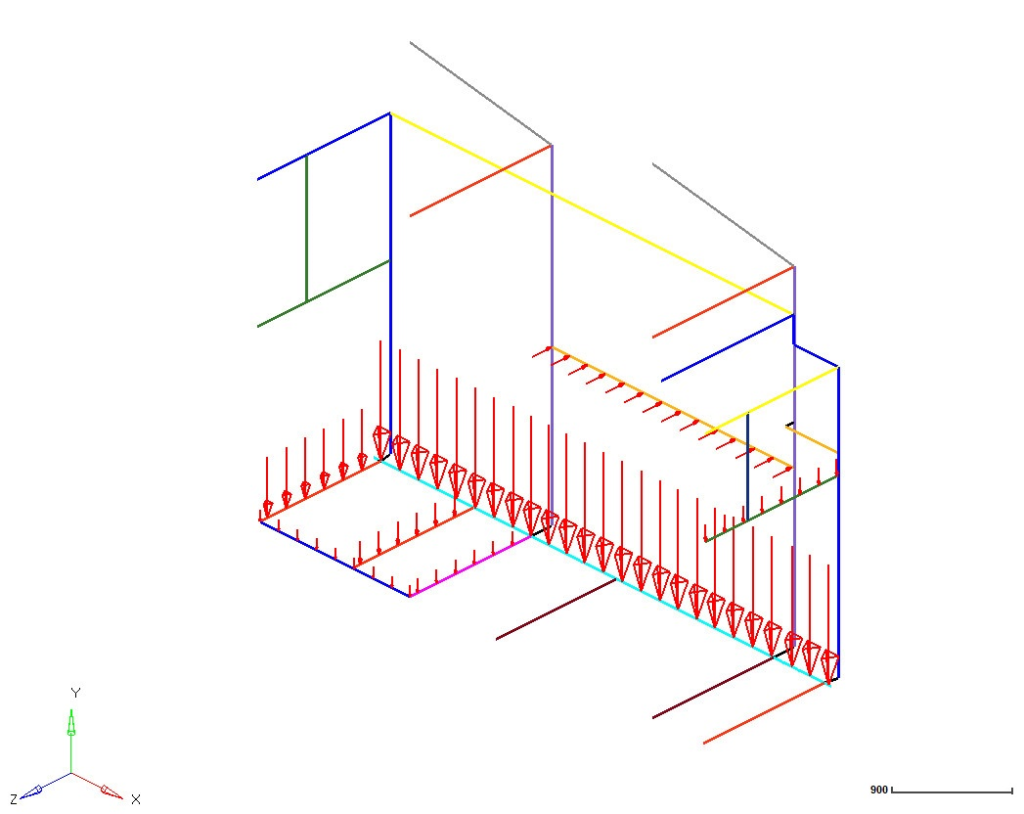
Fonte: OTMZA (2019)

Para simular o içamento por cabos foi utilizado o elemento de barra que permite somente esforços axiais. A conexão entre o cabo e a estrutura foi considerada como rotulada, pois o mesmo não resiste a solicitações não alinhadas com seu eixo. Por fim, as demais conexões entre os perfis foram consideradas rígidas.

Nas conexões entre perfis que não possuem centros de cisalhamento concorrentes, foram realizadas com elementos RBE2. Estes elementos transmitem todos os graus de movimento entre dois ou mais nós, simulando o comportamento de uma junta soldada. Enquanto que para as conexões em que os centros de cisalhamento são concorrentes isso foi feito conectando os elementos no mesmo nó.

O peso próprio da estrutura foi atribuído por um coletor de carga específico do software que, conforme a densidade do material e volume dos elementos, foi calculada a influência da gravidade no modelo.

 Parâmetros de Otimização Estrutural

Enfim, no processo de otimização paramétrica da estrutura foram utilizadas como variáveis de projeto as dimensões que definem as diferentes seções transversais de perfis:

• W: d (altura), bf (largura da mesa), tw (espessura da alma), tf (espessura da mesa);
• L: b (largura), t (espessura);
• U: d (altura), bf (largura da aba), tw (espessura da alma), tf (espessura da aba).

Representação das variáveis de projeto para perfis W, L e U respectivamente

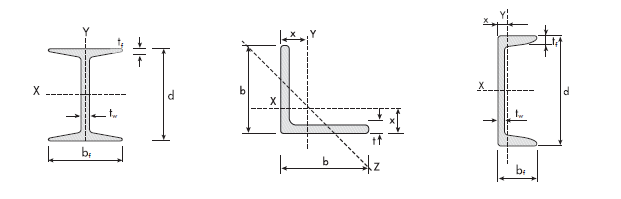
Fonte: OTMZA (2019)

A análise foi realizada utilizando o solver OptiStruct do pacote HyperWorks e a função objetivo foi definida como minimizar a massa da estrutura com duas restrições de tensão:

• Restrição de tensão máxima de von Mises para todos os elementos para manter o coeficiente de segurança da estrutura atual;
• Restrição de tensão axial de compressão para os perfis horizontais em contato com os cabos, com intuito de reduzir a probabilidade de flambagem.

O solver OptiStruct utiliza o método dos gradientes para otimização estrutural, que lida com variáveis contínuas. Assim, em perfis comerciais, os valores nominais são discretos e, para isso, foi utilizada uma ferramenta que ajusta resultados em variáveis contínuas para valores discretos. Além disso, foi utilizada a função DGLOBAL do software, que tem o objetivo de encontrar o mínimo global. Em suma, é o menor resultado para a função objetivo dentro do espaço viável de soluções, o que garante a menor massa possível de projeto dentro das restrições estabelecidas.

Resultados da Otimização Estrutural

Por fim, as análises resultantes foram do tipo estática estrutural e baseadas na tensão equivalente de von Mises. Dessa forma, seguindo os procedimentos e critérios expostos nas seções anteriores, foi obtida a resposta abaixo, indicando os perfis ideais para as condições impostas.

Perfis comerciais para a estrutura otimizada

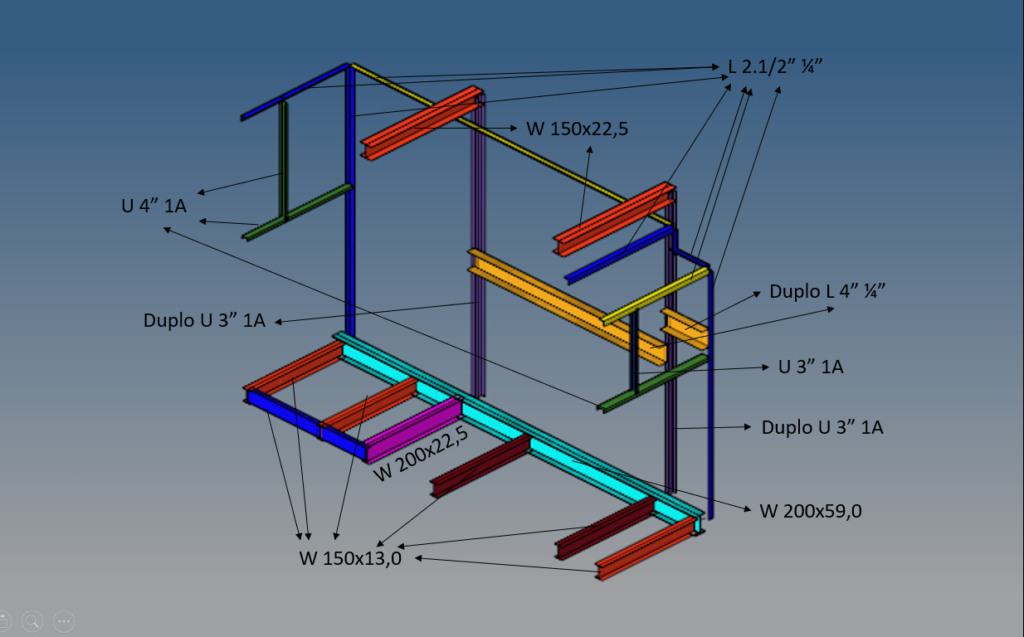
Fonte: OTMZA (2019)